Impedance Matching :-
Because transformers can step voltage and current to different levels, and because power is transferred equivalently between primary and secondary windings, they can be used to “convert” the impedance of a load to a different level. That last phrase deserves some explanation, so let’s investigate what it means.
The purpose of a load (usually) is to do something productive with the power it dissipates. In the case of a resistive heating element, the practical purpose for the power dissipated is to heat something up.
Loads are engineered to safely dissipate a certain maximum amount of power, but two loads of equal power ratings are not necessarily identical. Consider these two 1000 watt resistive heating elements:

Heating elements dissipate 1000 watts, at different voltage and current ratings.
Both heaters dissipate exactly 1000 watts of power, but they do so at different voltage and current levels (either 250 volts and 4 amps, or 125 volts and 8 amps). Using Ohm’s Law to determine the necessary resistance of these heating elements (R=E/I), we arrive at figures of 62.5 Ω and 15.625 Ω, respectively.
If these are AC loads, we might refer to their opposition to current in terms of impedance rather than plain resistance, although in this case, that’s all they’re composed of (no reactance). The 250-volt heater would be said to be a higher impedance load than the 125-volt heater.
If we desire to operate the 250-volt heater element directly on a 125-volt power system, we would end up being disappointed. With 62.5 Ω of impedance (resistance), the current would only be 2 amps (I=E/R; 125/62.5), and the power dissipation would only be 250 watts (P=IE; 125 x 2), or one-quarter of its rated power.
The impedance of the heater and the voltage of our source would be mismatched, and we couldn’t obtain the full rated power dissipation from the heater.
All hope is not lost, though. With a step-up transformer, we could operate the 250 volt heater element on the 125 volt power system like the Figure below.

Step-up transformer operates 1000 watt 250 V heater from 125 V power source.
Impedance, Current and Voltage Transformation Ratios :-
The ratio of the transformer’s windings provides the voltage step-up and current step-down we need for the otherwise mismatched load to operate properly on this system. Take a close look at the primary circuit figures: 125 volts at 8 amps. As far as the power supply “knows,” its powering a 15.625 Ω (R=E/I) load at 125 volts, not a 62.5 Ω load!
The voltage and current figures for the primary winding are indicative of 15.625 Ω load impedance, not the actual 62.5 Ω of the load itself. In other words, not only has our step-up transformer transformed voltage and current, but it has transformed impedance as well.
The transformation ratio of impedance is the square of the voltage/current transformation ratio, the same as the winding inductance ratio:

This concurs with our example of the 2:1 step-up transformer and the impedance ratio of 62.5 Ω to 15.625 Ω (a 4:1 ratio, which is 2:1 squared). Impedance transformation is a highly useful ability of transformers, for it allows a load to dissipate its full rated power even if the power system is not at the proper voltage to directly do so.
Application of Maximum Power Transfer Theorem to Transformers :-
Recall from our study of network analysis the Maximum Power Transfer Theorem, which states that the maximum amount of power will be dissipated by a load resistance when that load resistance is equal to the Thevenin/Norton resistance of the network supplying the power. Substitute the word “impedance” for “resistance” in that definition and you have the AC version of that Theorem.
If we’re trying to obtain theoretical maximum power dissipation from a load, we must be able to properly match the load impedance and source (Thevenin/Norton) impedance together. This is generally more of a concern in specialized electric circuits such as radio transmitter/antenna and audio amplifier/speaker systems.
Let’s take an audio amplifier system and see how it works: (Figure below)

Amplifier with impedance of 500 Ω drives 8 Ω at much less than maximum power.
With an internal impedance of 500 Ω, the amplifier can only deliver full power to a load (speaker) also having 500 Ω of impedance. Such a load would drop higher voltage and draw less current than an 8 Ω speaker dissipating the same amount of power.
If an 8 Ω speaker were connected directly to the 500 Ω amplifier as shown, the impedance mismatch would result in very poor (low peak power) performance. Additionally, the amplifier would tend to dissipate more than its fair share of power in the form of heat trying to drive the low impedance speaker.
To make this system work better, we can use a transformer to match these mismatched impedances. Since we’re going from a high impedance (high voltage, low current) supply to a low impedance (low voltage, high current) load, we’ll need to use a step-down transformer:

Impedance matching transformer matches 500 Ω amplifier to 8 Ω speaker for maximum efficiency.
Description of Impedance Matching :-
To obtain an impedance transformation ratio of 500:8, we would need a winding ratio equal to the square root of 500:8 (the square root of 62.5:1, or 7.906:1).
With such a transformer in place, the speaker will load the amplifier to just the right degree, drawing power at the correct voltage and current levels to satisfy the Maximum Power Transfer Theorem and make for the most efficient power delivery to the load. The use of a transformer in this capacity is called impedance matching.
Anyone who has ridden a multi-speed bicycle can intuitively understand the principle of impedance matching. A human’s legs will produce maximum power when spinning the bicycle crank at a particular speed (about 60 to 90 revolutions per minute).
Above or below that rotational speed, human leg muscles are less efficient at generating power. The purpose of the bicycle’s “gears” is to impedance-match the rider’s legs to the riding conditions so that they always spin the crank at the optimum speed.
If the rider attempts to start moving while the bicycle is shifted into its “top” gear, he or she will find it very difficult to get moving. Is it because the rider is weak?
No, its because the high step-up ratio of the bicycle’s chain and sprockets in that top gear presents a mismatch between the conditions (lots of inertia to overcome) and their legs (needing to spin at 60-90 RPM for maximum power output).
On the other hand, selecting a gear that is too low will enable the rider to get moving immediately, but limit the top speed they will be able to attain. Again, is the lack of speed an indication of weakness in the bicyclist’s legs?
No, its because the lower speed ratio of the selected gear creates another type of mismatch between the conditions (low load) and the rider’s legs (losing power if spinning faster than 90 RPM). It is much the same with electric power sources and loads: there must be an impedance match for maximum system efficiency.
In AC circuits, transformers perform the same matching function as the sprockets and chain (“gears”) on a bicycle to match otherwise mismatched sources and loads.
Impedance Matching Transformers :-
Impedance matching transformers are not fundamentally different from any other type of transformer in construction or appearance. A small impedance-matching transformer (about two centimeters in width) for audio-frequency applications is shown in the following photograph:

Audio frequency impedance matching transformer.
Another impedance-matching transformer can be seen on this printed circuit board, in the upper right corner, to the immediate left of resistors R2and R1. It is labeled “T1”:

Printed circuit board mounted audio impedance matching transformer, top right.
Potential Transformers :-
Transformers can also be used in electrical instrumentation systems. Due to transformers’ ability to step up or step down voltage and current, and the electrical isolation they provide, they can serve as a way of connecting electrical instrumentation to high-voltage, high current power systems.
Suppose we wanted to accurately measure the voltage of a 13.8 kV power system (a very common power distribution voltage in American industry):

Direct measurement of high voltage by a voltmeter is a potential safety hazard.
Designing, installing, and maintaining a voltmeter capable of directly measuring 13,800 volts AC would be no easy task. The safety hazard alone of bringing 13.8 kV conductors into an instrument panel would be severe, not to mention the design of the voltmeter itself.
However, by using a precision step-down transformer, we can reduce the 13.8 kV down to a safe level of voltage at a constant ratio, and isolate it from the instrument connections, adding an additional level of safety to the metering system:

Instrumentation application:“Potential transformer” precisely scales dangerous high voltage to a safe value applicable to a conventional voltmeter.
Now the voltmeter reads a precise fraction, or ratio, of the actual system voltage, its scale set to read as though it were measuring the voltage directly.
The transformer keeps the instrument voltage at a safe level and electrically isolates it from the power system, so there is no direct connection between the power lines and the instrument or instrument wiring. When used in this capacity, the transformer is called a Potential Transformer, or simply PT.
Potential transformers are designed to provide as accurate a voltage step-down ratio as possible. To aid in precise voltage regulation, loading is kept to a minimum: the voltmeter is made to have high input impedance so as to draw as little current from the PT as possible.
As you can see, a fuse has been connected in series with the PTs primary winding, for safety and ease of disconnecting the PT from the circuit.
A standard secondary voltage for a PT is 120 volts AC, for full-rated power line voltage. The standard voltmeter range to accompany a PT is 150 volts, full-scale.
PTs with custom winding ratios can be manufactured to suit any application. This lends itself well to industry standardization of the actual voltmeter instruments themselves, since the PT will be sized to step the system voltage down to this standard instrument level.
Current Transformers :-
Following the same line of thinking, we can use a transformer to step down current through a power line so that we are able to safely and easily measure high system currents with inexpensive ammeters. Of course, such a transformer would be connected in series with the power line.
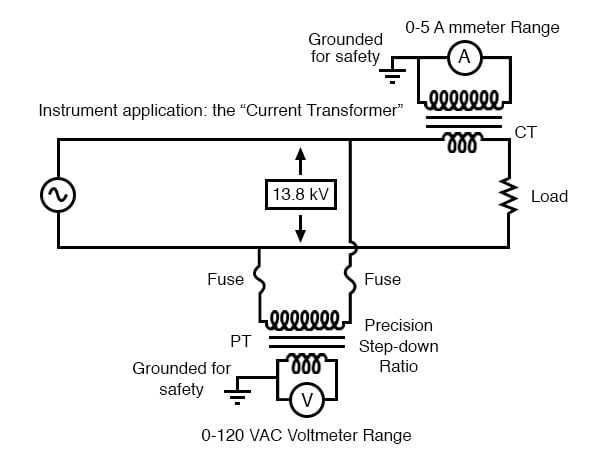
Instrumentation application: “Current transformer” steps high current down to a value applicable to a conventional ammeter.
Note that while the PT is a step-down device, the Current Transformer (or CT) is a step-up device (with respect to voltage), which is what is needed to step down the power line current. Quite often, CTs are built as donut-shaped devices through which the power line conductor is run, the power line itself acting as a single-turn primary winding:

Current conductor to be measured is threaded through the opening. Scaled down current is available on wire leads.
Some CTs are made to hinge open, allowing insertion around a power conductor without disturbing the conductor at all. The industry standard secondary current for a CT is a range of 0 to 5 amps AC. Like PTs, CTs can be made with custom winding ratios to fit almost any application.
Because their “full load” secondary current is 5 amps, CT ratios are usually described in terms of full-load primary amps to 5 amps, like this:

The “donut” CT shown in the photograph has a ratio of 50:5. That is, when the conductor through the center of the torus is carrying 50 amps of current (AC), there will be 5 amps of current induced in the CT’s winding.
Because CTs are designed to be powering ammeters, which are low-impedance loads, and they are wound as voltage step-up transformers, they should never, ever be operated with an open-circuited secondary winding.
Failure to heed this warning will result in the CT producing extremely high secondary voltages, dangerous to equipment and personnel alike. To facilitate maintenance of ammeter instrumentation, short-circuiting switches are often installed in parallel with the CT’s secondary winding, to be closed whenever the ammeter is removed for service:
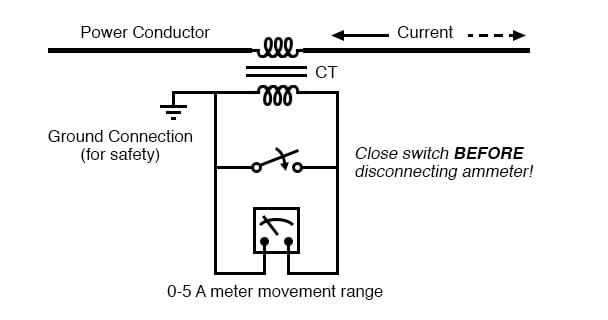
Short-circuit switch allows ammeter to be removed from an active current transformer circuit.
Though it may seem strange to intentionally short-circuit a power system component, it is perfectly proper and quite necessary when working with current transformers.
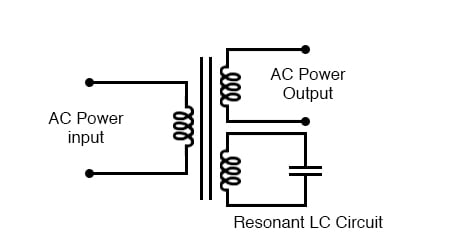
Air Core Transformers :-
Another kind of special transformer, seen often in radio-frequency circuits, is the air core transformer. True to its name, an air core transformer has its windings wrapped around a nonmagnetic form, usually a hollow tube of some material.
The degree of coupling (mutual inductance) between windings in such a transformer is many times less than that of an equivalent iron-core transformer, but the undesirable characteristics of a ferromagnetic core (eddy current losses, hysteresis, saturation, etc.) are completely eliminated.
It is in high-frequency applications that these effects of iron cores are most problematic.

Air core transformers may be wound on cylindrical (a) or toroidal (b) forms. Center tapped primary with secondary (a). Bifilar winding on toroidal form (b).
The inside tapped solenoid winding, without the over winding, could match unequal impedances when DC isolation is not required. When isolation is required the over winding is added over one end of the main winding. Air core transformers are used at radio frequencies when iron core losses are too high.
Frequently air core transformers are paralleled with a capacitor to tune it to resonance. The over winding is connected between a radio antenna and ground for one such application. The secondary is tuned to resonance with a variable capacitor.
The output may be taken from the tap point for amplification or detection. Small millimeter size air core transformers are used in radio receivers. The largest radio transmitters may use meter sized coils. Unshielded air core solenoid transformers are mounted at right angles to each other to prevent stray coupling.
Stray coupling is minimized when the transformer is wound on a toroid form. Toroidal air core transformers also show a higher degree of coupling, particularly for bifilar windings. Bifilar windings are wound from a slightly twisted pair of wires.
This implies a 1:1 turns ratio. Three or four wires may be grouped for 1:2 and other integral ratios. Windings do not have to be bifilar. This allows arbitrary turns ratios. However, the degree of coupling suffers. Toroidal air core transformers are rare except for VHF (Very High Frequency) work.
Core materials other than air such as powdered iron or ferrite are preferred for lower radio frequencies.
Tesla Coil :-
One notable example of an air-core transformer is the Tesla Coil, named after the Serbian electrical genius Nikola Tesla, who was also the inventor of the rotating magnetic field AC motor, polyphase AC power systems, and many elements of radio technology.
The Tesla Coil is a resonant, high-frequency step-up transformer used to produce extremely high voltages.
One of Tesla’s dreams was to employ his coil technology to distribute electric power without the need for wires, simply broadcasting it in the form of radio waves which could be received and conducted to loads by means of antennas.
The basic schematic for a Tesla Coil is shown in the Figure below.

Tesla Coil: A few heavy primary turns, many secondary turns.
The capacitor, in conjunction with the transformer’s primary winding, forms a tank circuit. The secondary winding is wound in close proximity to the primary, usually around the same nonmagnetic form. Several options exist for “exciting” the primary circuit, the simplest being a high-voltage, low-frequency AC source and spark gap:

System level diagram of Tesla coil with spark gap drive.
The purpose of the high-voltage, low-frequency AC power source is to “charge” the primary tank circuit. When the spark gap fires, its low impedance acts to complete the capacitor/primary coil tank circuit, allowing it to oscillate at its resonant frequency.
The “RFC” inductors are “Radio Frequency Chokes,” which act as high impedances to prevent the AC source from interfering with the oscillating tank circuit.
The secondary side of the Tesla coil transformer is also a tank circuit, relying on the parasitic (stray) capacitance existing between the discharge terminal and earth ground to complement the secondary winding’s inductance.
For optimum operation, this secondary tank circuit is tuned to the same resonant frequency as the primary circuit, with energy exchanged not only between capacitors and inductors during resonant oscillation, but also back-and-forth between primary and secondary windings. The visual results are spectacular:

High voltage high frequency discharge from Tesla coil.
Tesla Coils find application primarily as novelty devices, showing up in high school science fairs, basement workshops, and the occasional low budget science-fiction movie.
It should be noted that Tesla coils can be extremely dangerous devices. Burns caused by radio-frequency (“RF”) current, like all electrical burns, can be very deep, unlike skin burns caused by contact with hot objects or flames.
Although the high-frequency discharge of a Tesla coil has the curious property of being beyond the “shock perception” frequency of the human nervous system, this does not mean Tesla coils cannot hurt or even kill you! I strongly advise seeking the assistance of an experienced Tesla coil experimenter if you would embark on building one yourself.
Saturable Reactors :-
So far, we’ve explored the transformer as a device for converting different levels of voltage, current, and even impedance from one circuit to another. Now we’ll take a look at it as a completely different kind of device: one that allows a small electrical signal to exert control over a much larger quantity of electrical power. In this mode, a transformer acts as an amplifier.
The device I’m referring to is called a saturable-core reactor, or simply saturable reactor. Actually, it is not really a transformer at all, but rather a special kind of inductor whose inductance can be varied by the application of a DC current through a second winding wound around the same iron core.
Like the ferroresonant transformer, the saturable reactor relies on the principle of magnetic saturation. When a material such as iron is completely saturated (that is, all its magnetic domains are lined up with the applied magnetizing force), additional increases in current through the magnetizing winding will not result in further increases of magnetic flux.
Review on Inductance :-
Now, inductance is the measure of how well an inductor opposes changes in current by developing a voltage in an opposing direction. The ability of an inductor to generate this opposing voltage is directly connected with the change in magnetic flux inside the inductor resulting from the change in current, and the number of winding turns in the inductor.
If an inductor has a saturated core, no further magnetic flux will result from further increases in current, and so there will be no voltage induced in opposition to the change in current. In other words, an inductor loses its inductance (ability to oppose changes in current) when its core becomes magnetically saturated.
If an inductor’s inductance changes, then its reactance (and impedance) to AC current changes as well. In a circuit with a constant voltage source, this will result in a change in current:

If L changes in inductance, ZL will correspondingly change, thus changing the circuit current.
Saturable Reactor Operation :-
A saturable reactor capitalizes on this effect by forcing the core into a state of saturation with a strong magnetic field generated by current through another winding. The reactor’s “power” winding is the one carrying the AC load current, and the “control” winding is one carrying a DC current strong enough to drive the core into saturation:

DC, via the control winding, saturates the core. Thus, modulating the power winding inductance, impedance, and current.
The strange-looking transformer symbol shown in the above schematic represents a saturable-core reactor, the upper winding being the DC control winding and the lower being the “power” winding through which the controlled AC current goes.
Increased DC control current produces more magnetic flux in the reactor core, driving it closer to a condition of saturation, thus decreasing the power winding’s inductance, decreasing its impedance, and increasing current to the load. Thus, the DC control current is able to exert control over the AC current delivered to the load.
The circuit shown would work, but it would not work very well. The first problem is the natural transformer action of the saturable reactor: AC current through the power winding will induce a voltage in the control winding, which may cause trouble for the DC power source.
Also, saturable reactors tend to regulate AC power only in one direction: in one half of the AC cycle, the mmf’s from both windings add; in the other half, they subtract. Thus, the core will have more flux in it during one half of the AC cycle than the other and will saturate first in that cycle half, passing load current more easily in one direction than the other.
Fortunately, both problems can be overcome with a little ingenuity:
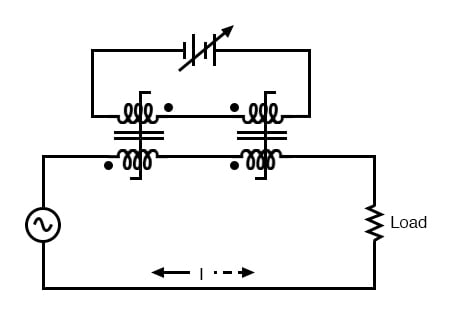
Out of phase DC control windings allow symmetrical of control AC.
Notice the placement of the phasing dots on the two reactors: the power windings are “in phase” while the control windings are “out of phase.” If both reactors are identical, any voltage induced in the control windings by load current through the power windings will cancel out to zero at the battery terminals, thus eliminating the first problem mentioned.
Furthermore, since the DC control current through both reactors produces magnetic fluxes in different directions through the reactor cores, one reactor will saturate more in one cycle of the AC power while the other reactor will saturate more in the other, thus equalizing the control action through each half-cycle so that the AC power is “throttled” symmetrically.
This phasing of control windings can be accomplished with two separate reactors as shown, or in a single reactor design with intelligent layout of the windings and core.
Saturable reactor technology has even been miniaturized to the circuit-board level in compact packages more generally known as magnetic amplifiers.
I personally find this to be fascinating: the effect of amplification (one electrical signal controlling another), normally requiring the use of physically fragile vacuum tubes or electrically “fragile” semiconductor devices, can be realized in a device both physically and electrically rugged.
Magnetic amplifiers do have disadvantages over their more fragile counterparts, namely size, weight, nonlinearity, and bandwidth (frequency response), but their utter simplicity still commands a certain degree of appreciation, if not practical application.
Saturable-core reactors are less commonly known as “saturable-core inductors” or transductors.
Scott-T Transformer :-
Nikola Tesla’s original polyphase power system was based on simple to build 2-phase components. However, as transmission distances increased, the more transmission line efficient 3-phase system became more prominent. Both 2-φ and 3-φ components coexisted for a number of years.
The Scott-T transformer connection allowed 2-φ and 3-φ components like motors and alternators to be interconnected. Yamamoto and Yamaguchi:
In 1896, General Electric built a 35.5 km (22 mi) three-phase transmission line operated at 11 kV to transmit power to Buffalo, New York, from the Niagara Falls Project. The two-phase generated power was changed to three-phase by the use of Scott-T transformations.

Scott-T transformer converts 2-φ to 3-φ, or vice versa.
The Scott-T transformer set, Figure above, consists of a center tapped transformer T1 and an 86.6% tapped transformer T2 on the 3-φ side of the circuit. The primaries of both transformers are connected to the 2-φ voltages.
One end of the T2 86.6% secondary winding is a 3-φ output, the other end is connected to the T1 secondary center tap. Both ends of the T1 secondary are the other two 3-φ connections.
Application of 2-φ Niagara generator power produced a 3-φ output for the more efficient 3-φ transmission line. More common these days is the application of 3-φ power to produce a 2-φ output for driving an old 2-φ motor.
In the Figure below, we use vectors in both polar and complex notation to prove that the Scott-T converts a pair of 2-φ voltages to 3-φ. First, one of the 3-φ voltages is identical to a 2-φ voltage due to the 1:1 transformer T1 ratio, VP12= V2P1.
The T1 center tapped secondary produces opposite polarities of 0.5V2P1 on the secondary ends.
This ∠0° is vectorially subtracted from T2 secondary voltage due to the KVL equations V31, V23.
The T2 secondary voltage is 0.866V2P2 due to the 86.6% tap. Keep in mind that this 2nd phase of the 2-φ is ∠90°. This 0.866V2P2 is added at V31, subtracted at V23 in the KVL equations.

Scott-T transformer 2-φ to 3-φ conversion equations.
We show “DC” polarities all over this AC only circuit, to keep track of the Kirchhoff voltage loop polarities. Subtracting ∠0° is equivalent to adding ∠180°. The bottom line is when we add 86.6% of ∠90° to 50% of ∠180°we get ∠120°. Subtracting 86.6% of ∠90° from 50% of ∠180° yields ∠-120° or ∠240°.

Graphical explanation of equations in Figure previous.
In Figure above we graphically show the 2-φ vectors at (a). At (b) the vectors are scaled by transformers T1 and T2 to 0.5 and 0.866 respectively. At (c) 1∠120° = -0.5∠0° + 0.866∠90°, and 1∠240° = -0.5∠0° - 0.866∠90°. The three output phases are 1∠120° and 1∠240° from (c), along with input 1∠0° (a).
Linear Variable Differential Transformer :-
A linear variable differential transformer (LVDT) has an AC driven primary wound between two secondaries on a cylindrical air core form (figure below). A movable ferromagnetic slug converts the displacement to a variable voltage by changing the coupling between the driven primary and secondary windings.
The LVDT is a displacement or distance measuring transducer. Units are available for measuring displacement over a distance of a fraction of a millimeter to a half a meter. LVDT’s are rugged and dirt resistant compared to linear optical encoders.

LVDT: linear variable differential transformer.
The excitation voltage is in the range of 0.5 to 10 VAC at a frequency of 1 to 200 Khz. A ferrite core is suitable at these frequencies. It is extended outside the body by an non-magnetic rod. As the core is moved toward the top winding, the voltage across this coil increases due to increased coupling, while the voltage on the bottom coil decreases.
If the core is moved toward the bottom winding, the voltage on this coil increases as the voltage decreases across the top coil. Theoretically, a centered slug yields equal voltages across both coils. In practice leakage inductance prevents the null from dropping all the way to 0 V.
With a centered slug, the series-opposing wired secondaries cancel yielding V13 = 0. Moving the slug up increases V13. Note that it is in-phase with with V1, the top winding, and 180° out of phase with V3, bottom winding.
Moving the slug down from the center position increases V13. However, it is 180° out of phase with with V1, the top winding, and in-phase with V3, bottom winding. Moving the slug from top to bottom shows a minimum at the center point, with a 180° phase reversal in passing the center.
REVIEW :-
- Transformers can be used to transform impedance as well as voltage and current. When this is done to improve power transfer to a load, it is called impedance matching.
- A Potential Transformer (PT) is a special instrument transformer designed to provide a precise voltage step-down ratio for voltmeters measuring high power system voltages.
- A Current Transformer (CT) is another special instrument transformer designed to step down the current through a power line to a safe level for an ammeter to measure.
- An air-core transformer is one lacking a ferromagnetic core.
- A Tesla Coil is a resonant, air-core, step-up transformer designed to produce very high AC voltages at high frequency.
- A saturable reactor is a special type of inductor, the inductance of which can be controlled by the DC current through a second winding around the same core. With enough DC current, the magnetic core can be saturated, decreasing the inductance of the power winding in a controlled fashion.
- A Scott-T transformer converts 3-φ power to 2-φ power and vice versa.
- A linear variable differential transformer, also known as an LVDT, is a distance measuring device. It has a movable ferromagnetic core to vary the coupling between the excited primary and a pair of secondaries.